Парадокс як стиль мислення древніх

Ми публікуємо окремі глави з книги Костянтина Узбека "Фрагменти побудови античної науки, філософії і культури", яка щойно вийшла друком за сприяння Донецького відділення наукового товариства ім. Шевченка та Союзу греків України

Наука як частина загальнолюдської історії розвивається паралельно з розвитком людського суспільства. Розглядаючи світобудову, світовий космос як щось хаотичне й прагнучи розібратися в цьому хаосі, яким править якийсь абстрактний розум (нус), давні мислителі прагнули виробити певний стиль мислення, встановити закономірності явищ, що відбуваються в навколишньому світі. Догрецька наука носила емпірико-догматичний характер. Але вона залишила багатий емпіричний матеріал, який необхідно було дедуктивно довести й філософськи обґрунтувати. Цю велику роль виконала давньогрецька наука. Прагнучи до встановлення загального порядку й знаходження закономірностей світобудови, давньогрецькі мислителі виявили протиріччя (парадокси) і намагалися їх певним чином вирішити. Цей парадоксальний (суперечливий) стиль мислення наклав свій відбиток на мислителів всіх наступних поколінь. Найбільшою заслугою цих поколінь мислителів був розвиток теоретичної науки. "Теоретичне мислення кожної епохи... – це історичний продукт, що приймає в різні часи дуже різні форми й разом з тим дуже різний зміст. Отже, наука про мислення, як і будь-яка інша наука, є історична наука про історичний розвиток людського мислення" [7, с. 26]. Біля витоків такого теоретичного знання стояв Фалес Мілетський (VІ–V ст. до н.е.), основоположник Мілетської школи, математик і філософ, один із семи мудреців Давньої Греції.

Але докази Фалеса мали предметний характер. Більш абстрактні форми математика одержала в піфагорійській школі. Відповідно до вчення Піфагора (580–500 рр. до н.е.), число є сутністю речей, математичні абстракції таємниче керують світом, установлюючи в ньому певний порядок. Числа визнавалися не просто вираженням закономірного порядку, але й суттю матеріального світу. Вчення Піфагора і його учнів стосувалося геометрії, теорії чисел, астрономії й інших наук. Але найбільше вони цінували результати, отримані в теорії гармонії. Так, піфагорійці встановили, що якщо довжини струн співвідносяться як 3 : 4 : 6, то вони дають найбільш гармонійний акорд, особливе звучання. Велике значення піфагорійці надавали "золотому перетину". Вони вважали, що пропорції, установлені за допомогою цього перетину, найбільш досконалі. Але незважаючи на те, що вони прагнули до встановлення гармонії в навколишньому світі й у математичних висновках, в остаточному підсумку вони прийшли до протиріччя в результаті доказу теореми, що встановлює залежність між сторонами прямокутного трикутника с2 = а2 + b2 (квадрат гіпотенузи дорівнює сумі квадратів катетів – теорема Піфагора). Ця теорема привела до першої кризи основ математики й усієї філософської системи піфагорійців. Як відомо, піфагорійці вважали числа суттю речей. Якщо існує число, то існує й річ, що характеризується даним числом. Зворотного твердження вони не визнавали, тобто число було первинним щодо речі. Але з доказом теореми Піфагора й одержанням залежності с2 = а2 + b2 стали з'являтися числа, відмінні від раціональних, раніше невідомі, не використовувані піфагорійцями – ірраціональні числа. Виниклі протиріччя привели до кризи основ математики й усієї піфагорійської філософської системи. Вихід з кризи основ математики став можливим пізніше, завдяки роботам Евдокса Кнідського (408–355 рр. до н.е.) і його учнів. Математика перейшла з дискретної на континуальну основу. Основою в математиці визнавалося не число, а величина, під якою розумівся деякий прямолінійний відрізок, що міг безупинно змінюватися. Вимірювався він з будь-яким ступенем точності за допомогою інших відрізків. Розроблений Евдоксом Кнідським "метод вичерпання" є найвидатнішим творінням математики за всю її історію" [2, с. 197], він дав можливість розв’язати протиріччя, які виникли у результаті доведення теореми Піфагора, і подолання першої кризи її основ.

На особливу увагу заслуговують апорії Зенона Елейського (бл. 490–430 р. до н.е.) і суперечливий стиль його мислення, що за допомогою парадоксальних доведень піддавав істини сумніву. Він висунув 45 апорій (протиріч, парадоксів), з яких до нас дійшли 9. Його апорії спрямовані проти множинності, нескінченності й руху. Чотири з апорій, які дійшли до нас, іменуються апоріями руху, це апорії "Ахілес і черепаха", "Стріла, що летить", "Дихотомія", "Стадії". Так, у апорії "Ахілес і черепаха" стверджується, що швидконогий Ахілес ніколи не наздожене черепахи, тому що поки він пройде відстань до черепахи, черепаха за цей час пройде деяку відстань, після проходження ним цього нового шляху черепаха пройде новий відрізок шляху й т. і. За логікою суджень цей процес нескінченний, тому що черепаха увесь час буде випереджати Ахілеса й буде проходити певну відстань, перш ніж Ахілес пройде попередню відстань. Але в дійсності виходить інакше. Ахілес, маючи більшу швидкість, повинен обігнати черепаху. Парадокс полягає в логіці суджень, яка не відповідає реальній дійсності.

Якщо проаналізувати судження Зенона в апорії "Дихотомія", то прийдемо до того, що рух узагалі відсутній. Щоб пройти відрізок усього шляху, необхідно пройти спочатку першу його половину, а щоб пройти першу половину, необхідно пройти чверть, потім – восьму й т.д. нескінченно. Отже, щоб пройти відрізок певної довжини, необхідно пройти нескінченну кількість відрізків, сума яких дорівнює

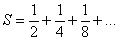
Отже, щоб пройти весь відрізок, потрібна нескінченна безліч відрізків часу, що практично неможливо. Із цієї логіки суджень виходить, що рух неможливий. У цьому плані також вступають у протиріччя дійсний факт і логіка суджень.

Така логіка суджень настійно вимагала розробки нових методів переходу від дискретних (перервних) до континуальних (неперервних) основ, від кінцевих множин до нескінченного й уведення граничного переходу. Аргументи Зенона Елейського також приводили давньогрецьку математику до кризового стану й настійно порушували питання про розвиток діалектичного способу мислення. Математика зокрема й наука взагалі в цей час розвивалася на основі математичного атомізму Піфагора й фізичного атомізму Левкіппа-Демокрита, у науковий обіг увійшли діалектичні методи й безперервність (континуальність). Основне положення, відстоюване Зеноном і Парменідом (учитель Зенона), полягає в тому, що перервність, множинність і рух – характеристики видимої, чуттєво сприйманої картини миру. Але ця картина світу, на їхню думку, не є достовірною: істинна картина світу осягається умоглядно, безпосередньо логікою мислення. Спроба мислити про множинність світів приводить до протиріччя. Якщо виходити із цієї множинної картини світу, то сума нескінченної безлічі малих величин приведе до нескінченно великої, необмеженої величини. Такий постулат є помилковим у сучасній математиці. На підставі граничного переходу, розробленого французьким математиком Огюстеном Коші й німецьким – Карлом Вейєрштрассом, були встановлені певні закономірності в діях над нескінченно малими й нескінченно великими величинами. Але заслуга Зенона Елейського полягає в тому, що він поставив ці завдання й установив протиріччя.

Завдання відображення руху носить суперечливий, діалектичний характер. Зенон і не думав спростовувати існування руху, питання полягає в тому, як виразити його в логіці понять.

Наведені приклади показують, що при вивченні будь-якого процесу спостерігається взаємодія кінечного й нескінченного, дискретного й безперервного. Процес, що розвивається діалектично, необхідно призупинити, вивчати в спокої, далі необхідно вивчити діалектично суперечливий взаємозв'язок між його елементами, взаємне проникнення протилежностей і виявлення тенденції розвитку цього процесу.

Апорії Зенона Елейського не втратили свого значення й у наші дні, тому що вони належать до основних законів діалектики й руху, до складних проблем основ математики, пов'язаних з абстракціями актуальної й потенційної безкінечності.

Діалектика суперечливих суджень проникла повсюдно в життя давньогрецького суспільства. Вона проявилася в мистецтві ведення суперечки, у діалогах повсякденного життя, у судових процесах, у наукових диспутах. Переслідувалася одна мета – досягнення істини. Для цього необхідно було вигострювати логіку мислення, логічну побудову діалогу, дискусії.

Виняткового значення мистецтву ведення суперечок (дискусій) надавав Сократ. Він не визнавав наукових праць, уважав, що неможливо відобразити, виразити в працях той діалог, що може виникнути в суперечці, наблизити його до істини. Важко заздалегідь передбачити ті проблеми, які можуть виникнути в суперечці. Сократ стверджував, що діалог – справжня, жива й одушевлена мова тямущої людини, писемність же – це всього лише "наслідування діалогу". У письмових творах, вважав Сократ, легше уникнути видимих протиріч, згладжуючи гострі кути, а в суперечці, у протиріччях народжується істина. Але це однобічний підхід. Неможливо розвивати науку без писемності, без акумуляції знань у писаннях, творах. Не записавши основних наукових висновків, можна втратити їх безповоротно.

У діалозі Сократ виступав не в ролі вчителя, а в ролі співрозмовника, найбільше він цінував майстерність задавати питання, які, на його думку, приводили до народження істини в голові співрозмовника. Цей метод питально-відповідного діалогу, що одержав назву методу "майєвтики", найчастіше заганяв співрозмовника в глухий кут, і співрозмовник вступав у протиріччя із самим собою. Сократ підбирав питання таким чином, щоб, коли співрозмовникові доводилося на них відповідати, він спростовував попереднє твердження. Цей метод "майєвтики" або сократівських "пасток" став класичним методом у різних діалогах. У методах ведення суперечки Сократа порівнювали зі скатом, з ґедзем, у тому розумінні, що, бентежачи інших, він сам заходить на слизьке. Але, активізуючи в такий спосіб співрозмовника, він змушує його помізкувати, наблизитися до істини. Через це Сократ не залишив письмової наукової й літературної спадщини. Про його наукові здобутки свідчать письмові праці його учнів, істориків, коментаторів, в основному Платона, Ксенофонта, Аристотеля. Але метод ведення діалогу, суперечки, спростування, приведення до протиріччя, названий методом "майєвтики" або сократівської "пастки", як згодом назвали цей метод, широко використовувався мислителями наступних поколінь.

Наукова дискусія, у яку Сократ прагнув утягти співрозмовника, являла собою розумовий експеримент. На початку діалогу Сократ намагався уточнити основні поняття й визначення, розвиваючи логіку мислення й користуючись індукцією, прагнув підвести співрозмовника до істини.

Такий метод спростування, тобто приведення до протиріччя за рецептом Зенона Елейського й Сократа, знайшов застосування й у математиці, як класичний метод доведення від противного. Для доведення певного положення робиться спроба спростувати твердження, яке формулюється в теоремі. Але якщо при цьому приходимо до безглуздості, до протиріччя, то твердження теореми вірне, а його спростування невірне [4, с. 62]. Аналізуючи основні положення й методи побудови окремих наук, у тому числі й математики, можна прийти до наступного висновку: основні поняття, їх першооснови, форми суджень і методи побудови розроблялися у філософських школах. Аристотель відзначає, що "... досліджувати те, що становить привхідні властивості сущого як такого й протилежності його як сущого, – це справа не якої-небудь іншої науки, а тільки філософії", і далі: "Хоча математик на свій розсуд і користується загальними положеннями, але засади математики першою має досліджувати філософія" [1, с. 278]. Аристотель визначає математику й науку про природу (перша філософія) як умоглядні науки, які переважніші за інших. Але до математики він підходить диференційовано, розглядаючи її за розділами (арифметика, геометрія, астрономія), кожний з яких займається певною сутністю, "а загальна математика простирається на всі" [1, с. 182].

Йдучи за Аристотелем, можна відзначити, що математики, створюючи свої теоретичні побудови, використовують філософські висновки, тому що методи, розроблені філософами, мають загальний характер і придатні для всіх інших наук. Такі першооснови теоретичної математики як визначення, аксіоми, постулати, означувані й неозначувані поняття та ін., розроблялися в диспутах філософських шкіл. Вважалося, що структурна їх побудова – справа не математиків, а філософів. Прагнучи "обійти" парадоксальні явища, філософи будували такі логічні конструкції, які використовувалися потім у побудовах теоретичної математики. Показовим є логіко-силогічна конструкція Аристотеля, що надалі була використана Евклідом у побудові знаменитих "Начал". Цей дедуктивний метод став загальновизнаним.

Але слід зазначити, що й математика своїми методами часто впливала на розвиток філософської думки й виводила її з кризової ситуації, наприклад вже згадувана теорія пропорцій Евдокса Кнідського.

Подальший розвиток математики відбувався на дискретній атомістичній і континуальній основі. З одного боку, математичний атомізм піфагорійців і фізичний атомізм Левкіппа-Демокрита дозволив вирішити багато завдань математики й природознавства, а з іншого – континуальна геометрична система сміливо входила в математику й стародавню науку. Розвиваючись паралельно, ці дві суперечні одна одній системи поглядів на навколишній світ привели до створення диференціального й інтегрального числення й обумовили вихід з другої кризи основ математики. Корені цих глибоких протиріч, як бачимо, були виявлені більше двох тисяч років тому давньогрецькими вченими, а їхнє вирішення зумовило новий якісний стрибок у науковому пізнанні.

Глибокі фундаментальні дослідження були проведені давньогрецькими дослідниками і в галузі логічних побудов. Логічні парадокси були виявлені ще за ІІ–ІІІ тисячоліття до н.е. Приклад – "парадокс брехуна", приписуваний Евбуліду. "Усі критяни – брехуни", – заявляє критянин. Якщо він говорить правду й він критянин, то він, щонайменше, один критянин, що говорить правду. Якщо він говорить неправду, тобто не всі критяни брехуни, а хтось говорить правду, то знову виходить парадокс.

Інший парадокс – це парадокс "купи". Одне зерно не є купою, а два, три, чотири й т.д. зерна чи будуть представляти купу? Починаючи з якого n+1 кількості зерен будемо мати купу? У результаті таких міркувань одержуємо парадоксальне явище, що ніколи не одержимо "купи", тобто множини. Але математично абстрагуючись від матеріальної дійсності й створюючи теоретико-множинний апарат математики, під множиною прийнято розуміти будь-яку сукупність, у тому числі й сукупність, що складається з одного, двох елементів і взагалі що не має жодного елемента – це множина, іменована порожньою множиною.

З особливою силою парадокси древніх проявилися в процесі розвитку формальної й математичної логіки, у теорії множин і різних логічних побудов. Вони постали перед науковим світом як парадокси Рассела, Рішара, Кантора, Буралі-Форті й інших. Бурхливий розвиток нових математичних методів, створення теорії множин і арифметизація математичного знання, як у фокусі, сконцентрували всі логіко-математичні протиріччя й парадокси. Ці парадокси мають багато загального з парадоксами типу "брехуна", "купи", апоріями Зенона, вони спрямовують думку дослідника на побудову нових теоретичних систем, що усувають ці протиріччя. Так, Е. Каснер і Д. Ньюмен у статті "Загублений і віднайдений парадокс" указують на одне із джерел появи парадоксів: "Зверніть увагу на слово "всіх" –якраз воно й небезпечне... Коли математик говорить, що якісь твердження істинні для певного об'єкта, то це цікаво й, напевно, безпечно. Але, коли він намагається поширити своє твердження на всі об'єкти, то, хоча це значно більш цікаво, але набагато небезпечніше. У переході від одного до всього, від спеціального до загального математика досягла своїх найбільших успіхів, але й наразилася на серйозні невдачі, найважливішу частину яких становлять логічні протиріччя" [3, с. 23-24].

Фон Нейман причиною парадоксів теорії множин уважав "елементність" множини. "Це означає, що причиною парадоксів є не існування надвеликих множин, а уявлення їх як членів інших множин" [6, с. 124].

Д. Гільберт вбачав усунення парадоксів у теорії множин і в будь-якій дедуктивній теорії в повній їх формалізації. Він пропонував формалізувати не тільки математичні символи й поняття, але й правила виведення. На його думку, математика повинна перетворитися на певну сукупність формул, з яких одна переходить в іншу за строгими правилами виведення, утворюючи тим самим замкнуту аксіоматичну систему. Але чи можна створити таку аксіоматичну систему, яка б вирішила всі протиріччя? Усередині самої аксіоматичної системи з'являються нерозв'язні елементи, приєднання яких до попередніх веде до розширення цієї аксіоматичної системи, а усередині розширеної аксіоматики також виникають недовідні й незаперечні елементи. Це зумовлює побудову нескінченної ієрархії аксіоматичних систем. Виходить, що кожна аксіоматика страждає на дедуктивну неповноту, вона не може довести всі позиції теорії.

Австрійський логік К. Гедель у своїх теоремах переконливо довів неповноту логічних систем. Він установив, що в будь-якій логічній побудові зустрічаються твердження, які неможливо ні спростувати, ні довести за допомогою раніше прийнятої аксіоматичної системи. Ці недовідні положення або можуть бути перевірені на практиці, або вони можуть бути доведені більш сильною аксіоматичною системою й включені в попередню. Таке розширення аксіоматичної системи приводить також до розширення її дедуктивних можливостей. Ці математичні побудови ще раз підтвердили суперечливість наукового пізнання.

Варто зупинитися ще на одному важливому моменті при побудові математичного знання, яким є рішення завдань на побудову. Як відомо, такого роду задачі вирішуються за допомогою циркуля й лінійки. Але за допомогою цих засобів виявилося неможливим вирішити три знамениті задачі, названі "трьома задачами старовини" – побудова квадрата, рівновеликого за площею даному кругу (задача про квадратуру круга), побудова куба, об’єм якого удвічі перевищує об’єм даного (задача про подвоєння об'єму куба) і розбиття кута на три рівні частини (задача про трисекцію кута). Але ці задачі виявилися розв'язними за допомогою інших, більш сильних аналітичних засобів. У XIX столітті було доведено, що всі три задачі нерозв'язні за допомогою циркуля та лінійки. Питання можливості побудови повністю вирішується алгебраїчними методами, основаними на теорії Галуа. Значимість "трьох знаменитих задач старовини" у математиці й у науці загалом велика, – вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, більш сильних, стала потужним поштовхом у розвитку математики, її основ і філософії. Здатність грецького генія до постановки таких суперечливих задач на багато тисячоріч визначила напрямок у розвитку людського знання як діалектично суперечливого наукового методу.

Неможливість побудови всеосяжної теорії в досягненні абсолютної істини, абсолютного, істинного знання знайшли широке відбиття й у філософських системах. Так, у піфагорійців це було представлене числовою характеристикою. Ідучи за піфагорійцями і Гераклітом Ефеським, Платон і його послідовники поставили у відповідність об'єктам світобудови "ейдоси" – недосяжні незмінні ідеї, а в проміжку між ними – математичні фігури. "Філософія Платона – це чудовий зразок не ранньої й не середньої, але вже зрілої класики, основним змістом якої й була діалектика ідеї й матерії як абстрактно-загальних категорій", – говорить О. Ф. Лосєв [5, с. 63].

Але Аристотель у науковому пізнанні визнає тільки те, що в кожному одиничному можливо знайти загальні принципи. Він надає значення усякій спільності, якщо вона діє, "рухається сама й надає руху матеріальним речам". Для нього "важлива не сама ідея, але її поточно-сутнісне становлення, її формуюча сила, її потенція, її енергія й породжуваний нею зорово-значеннєвий вигляд речі, який він називає ейдосом" [5, с. 69]. Таке прагнення осягти незбагненне за рахунок потенційно-енергійного та ейдетичного приводить його до породження ентелехії. Це – своєрідна незбагненна істина (нус), до якої спрямований людський розум. Але ентелехії Аристотеля, як і ейдоси Платона, до кінця незбагненні в пізнанні.

Подальший розвиток ці ідеї одержали у філософських системах І. Канта – як непізнавана "річ у собі", "абсолют" Г. Гегеля.

Прагнення до вирішення парадоксальних явищ і сьогодні приводить наукову думку до побудови цілих логіко-математичних конструктивних систем. Це ще раз переконує нас у тому, що парадокси древніх займають вузлові позиції в науковому пізнанні. І спроби їхнього вирішення приводять до подальшого розвитку наукового знання у різних напрямках. Геніальність давньогрецьких учених полягає в тому, що вони з найдавніших часів помітили ці нерозв'язні протиріччя, недостатність розв'язних засобів і поставили їх перед усім світом як проблеми класичного судження, можливість розв'язання яких приводить до різних модифікацій.

Підбиваючи підсумок наведеним судженням про теоретичну побудову наукового знання, слід зазначити, що жодна теорія не може бути всеосяжною, а всі проблеми, поставлені загальнолюдською практикою й мисленням, розв'язними. Будь-яка теоретична конструкція має обмежені можливості, але в науковому пізнанні вкоренився термін "криза" теорії, "тупик" теорії. На наш погляд, не "криза", не "тупик", а вичерпані можливості даної теорії приводять до парадоксальних суджень. Такі парадокси підштовхують свідомість учених до розробки нових наукових підходів, до побудови нових наукових теорій, які дають можливість уникати кризових ситуацій і на основі нових теоретичних побудов вивчати виникаючі проблеми й протиріччя.

Література

1. Аристотель. Метафизика / Аристотель // Сочинения : в 4 т. – М., 1976. – Т. 1.
2. Бородин А. И. Биографический словарь деятелей в области математики / А. И. Бородин, А. С. Бугай. – К., 1979.
3. Каснер Э. Потерянный и найденный парадокс / Э. Каснер, Д. Ньюмен // Математики о математике. – М., 1969.
4. Кессиди Ф. Х. Сократ / Ф. Х. Кессиди. – М., 1976.
5. Лосев А. Ф. История античной философии / А. Ф. Лосев. – М., 1989.
6. Френкель А. Основания теории множеств / А. Френкель, И. Бархиллел. – М., 1966.
7. Энгельс Ф. Диалектика природы / Ф. Энгельс. – М., 1982.

Опубліковано в науковому виданні "Філософсько-антропологічні студії". – 2001. – Спецвипуск. – С. 200–210.